Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Math 201 Test 3 Review

1. Know how to represent integers using color counters and the number line.

2. Know the definition and how to compute the absolute value.

3. Be able to add and subtract integers using color counters and the number line.

4. Be able to multiply integers using color counters and the number line. Know the definition for division
and be able to compute quotients.

5. Know how to add, subtract, and multiply on a clock. Be comfortable enough with this that you could
work on a clock other than a 12-hour clock.

6. Be able to describe and work with fractions using the colored regions model, fraction strips, and the
number line.

7. Be able to determine whether two fractions are equivalent or not.

8. Be able to add and subtract fractions and be prepared to explain why, using any conceptual model,
the addition algorithm works the way it does (i.e. finding a common denominator).

9. Be able to convert from an “improper” fraction to a mixed number and vice versa.

10. Be able to multiply fractions using a rectangular array. Be able to use this model to explain the
algorithm for multiplying fractions.

11. Be able to divide fractions using the algorithm.

12. Be able to solve conceptual word problems that involve division of fractions (like the math club pizza
problem from class where we drew pictures).

13. Be able to write word problems that correspond to fraction multiplication and division problems.

14. Know the definition of a rational number.

15. Know the density property for rational numbers.

16. Be able to find a rational number between two given rationals.

Practice Problems

1. Order the following rational numbers from least to greatest.

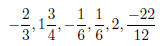
2. Find three rational numbers between

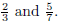
3. For the following, explain how to compute the problem using the indicated conceptual model.
(a) Model 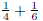using colored regions.
(b) Model 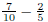using fraction strips.
(c) Model 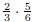using a rectangular array.

4. Use a conceptual model (i.e. draw a diagram) to show how to solve the following problem. Explain
your picture using complete sentences.
Each quart of soup calls for 2/3 cup of pinto beans. How many quarts of soup can be made with 3 cups
of beans?

5. The length of a day on Neptune is about 16 hours. The Neptunian children were doing arithmetic on
their 16 hour clock. Help them solve the following problems.

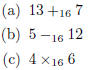
(d) What is the additive identity on the Neptunian clock?

6. Mark the following statements True or False
(a) 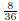and 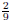are equivalent fractions.
(b) The integers are closed under addition, subtraction, multiplication, and division.
(c) If the rational numbers x and y are additive inverses of each other, then x × y = 1.
(d) If x is negative, then |x| = −x.

7. Explain, using complete sentences and color counters, why 3 − (−2) is the same as 3 + 2.

8. Use a number line to model the following problems.
(a) 5 + (−7)
(b) 5 − 7
(c) 5 − (−7)
(d) 2 × −3

9. Replace 5/6 and 7/9 by equivalent fractions with the least common denominator.

10. Use the GCD to find the simplest form of the fraction 24/60 .