Polynomial Equations and Symmetric Functions
While algorithms for solving polynomial equations of
degree at most 4 exist, there are in
general no such algorithms for polynomials of higher degree. A polynomial
equation to be
solved at an Olympiad is usually solvable by using the Rational Root Theorem
(see the
earlier handout Rational and irrational numbers), symmetry, special forms,
and/or
symmetric functions.
Here are, for the record, algorithms for solving 3rd and 4th degree equations.
Algorithm for solving cubic equations. The general cubic equation
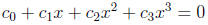
can be transformed (by dividing by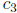 
and
letting 
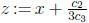) into an equation of the form
To solve this equation, we substitute x = u + v to obtain
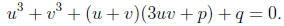
Note that we are free to restrict u and v so that
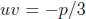. Then 
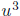and
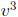are the roots
of the equation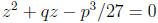 
. Solving this equation, we
obtain
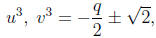
where
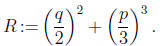
Now we may choose cube roots so that
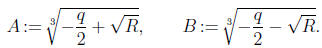
Then A + B is a solution. It is easily checked that the other pairs are obtained
by rotating
A and B in the complex plane by angles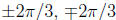 
. So,
the full set of solutions is
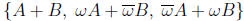where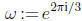 
:
Ferrari's method of solving quartic equations. The general quartic
equation is reduced
to a cubic equation called the resolvent. write the quartic equation as
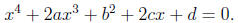
Transpose to obtain
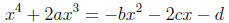
and then adding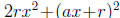 
to
both sides makes the left-hand side equal to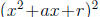 
.
If r can be chosen to make the right-hand side a perfect square, then it will be
easy to find
all solutions. The right-hand side,
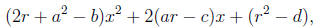
is a perfect square if and only if its discriminant is zero. Thus we require
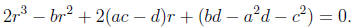
This is the cubic resolvent.
Reciprocal or palindromic equations. If the equation the form
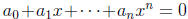
and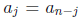 
for all j = 0,... ,n, it is called
palindromic. For even n, the transformation
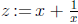reduces the equation to a new one of degree
n/2. After finding all solutions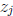 
,
the solutions of the original equation are found by solving quadratic equations
.
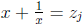Examples.
1. Solve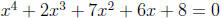 
.
2. Solve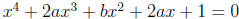 
.
3. Solve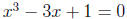 
.
4. Solve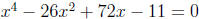 
.
5. Solve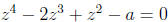 
and find values of a for which all
roots are real.
Definitions. A function of n variables is symmetric if it is invariant
under any permutation
of its variables. The kth elementary symmeric function is defined by
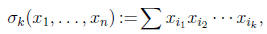
where the sum is taken over all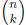 
choices of
the indices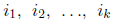
from the set
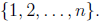
Symmetric function theorem. Every symmetric polynomial function of
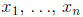is a
polynomial function of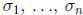 
. The same conclusion
holds with "polynomial" replaced
by "rational function".
Theorem. Let 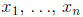be the roots of the
polynomial equation
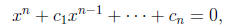
and let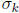 
be the kth elementary symmetric
function of 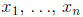. Then
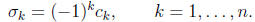
Newton's formula for power sums. Let
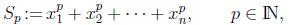
where 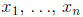are the roots of
Then
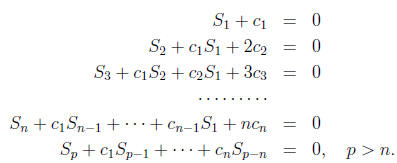
Examples.
1. Find all solutions of the system
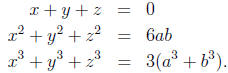
2. If
determine the value of 
.
3. Let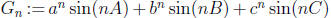 
, where a, b, c, A, B, C are real
numbers
and A+ B+ C is a multiple of π. Prove that if
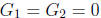, then 
for all k ∈ IN.
4. Find a cubic equation whose roots are the cubes of the roots of
.
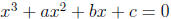5. Find all values of the parameter a such that all roots of the equation
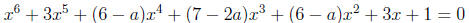
are real.
6. A student awoke at the end of an algebra class just in time to hear the
teacher say,
"...and I give you a hint that the roots form an arithmetic progression."
Looking at the
board, the student discovered a fifth degree equation to be solved for homework,
but
he had time to copy only
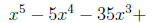
before the teacher erased the blackboard. He was able to find all roots anyway.
What
are the roots?