Simplifying Radical Expressions

In the last section every number under the square root symbol was a perfect square. When this
happens the radical sign disappears and entire square root is replaced with with a rational number.
When you find the square root of a perfect square there will not be a square root in the answer.

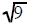was replaced with a 3

was replaced with a 5

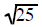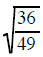was replaced with a 6/7

Most of the time the number under the square root is not a perfect square. The square root of any
number that is not a perfect square can't be replaced by any fraction, decimal or whole number. This
type of number is an irrational number. It represents a decimal that never ends or repeats. Since you
cannot write such a decimal you cannot replace such a square root as a number without a radical sign.

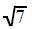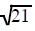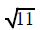cannot be replaced	cannot be replaced	cannot be replaced
with a decimal or fraction,	with a decimal or fraction,	with a decimal or fraction,
it stays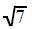	it stays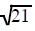	it stays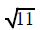

Some square roots can be reduced to the square root of a smaller number

If the number under the square root is not a perfect square then it cannot replaced with a number
without a radical sign. It may be replaced with an expression that has a smaller number under the
radical sign.

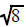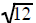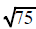can be replaced by	can be replaced by	can be replaced by

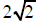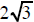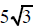We call the process of replacing one square root expression with another square root expression that
has a smaller number under the radical sign reducing or simplifying the square root.

Multiplication Rule for Square Roots

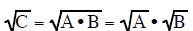
This rule allows you to factor a number under the square root into two (or more) factors and write the
factors as a product under two separate square roots. If one of the factors is a perfect square then that
square root can be reduced leaving you with a number outside the radical times a smaller square root
then the original square root you started with.

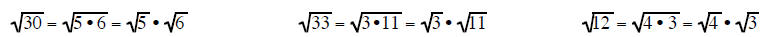
Simplifying Radicals using PERFECT SQUARE FACTORS

If you can find the largest perfect square factor of the radicand then reducing the radical expression is
a short process. It requires that you find the largest perfect square that is a factor of the original
radicand

Look for the largest perfect square that is a factor of the radicand. Factor than reduce.

Example 1	Example 2	Example 3

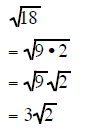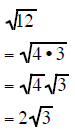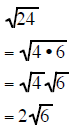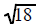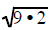Example 1 Note: To use this technique you must factorasand not as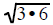

Example 4	Example 5	Example 6

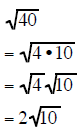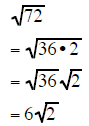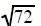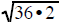Example 6 Note: To use this technique you must factorasand not as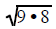
The factor must be the largest square root factor

Example 7	Example 8	Example 9
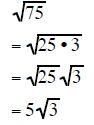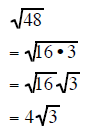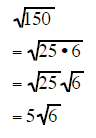Example 10	Example 11	Example 12

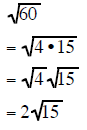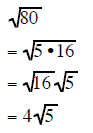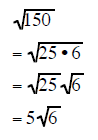Simplifying Radicals using PAIRS OF FACTORS

If you can find the largest perfect square factor of the radicand then reducing the radical expression is a
short process. Many students cannot find the largest perfect square factor or they do not want to take
the extended time this may take. There is a alternate approach that is favored by many students.

Two of the same factors under a square root form a perfect square. This means that if you have a pair
of the same factors under a square root they can be reduced to a rational number.

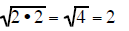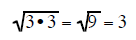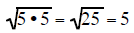a pair of 2's under a square root reduce to the whole number 2	a pair of 3's under a square root reduce to the whole number 3	a pair of 5's under a square root reduce to the whole number 5

This fact allows us to use the Multiplication Rule for Square Roots to completely factor a radicand into
its many factors and then take out the pairs of same factors

Example 1	Example 2	Example 3
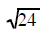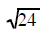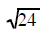completly factor 24	completly factor 24	completly factor 24
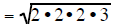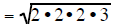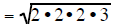put pairs of the same factor under thier own square root	put pairs of the same factor under thier own square root	put pairs of the same factor under thier own square root
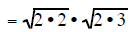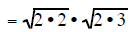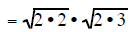the pair of 2's can reduced	the pair of 2's can reduced	the pair of 2's can reduced

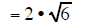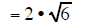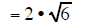Completely factor the radicand and take out all the pairs of factors:

Example 4	Example 5	Example 6
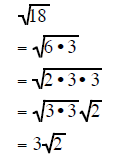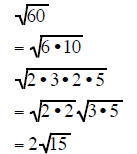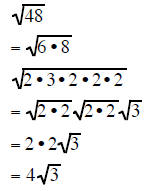Example 7	Example 8	Example 9
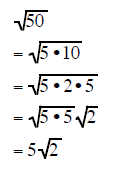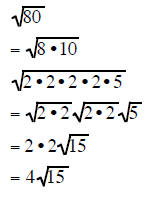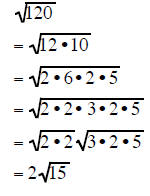Example 10	Example 11	Example 12
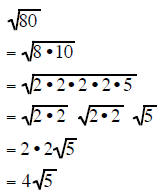
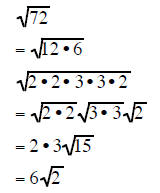
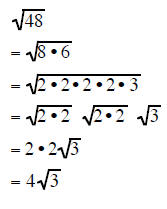