Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

ARITHMETIC WITH FRACTIONS, MIXED NUMBERS, AND PRIME NUMBERS

The problems below are relevant for Grades 3-7, or possibly 2-7. According
to the 2003 Minnesota Mathematics Standards, it is the goal of
Minnesota that students become fluent in the arithmetic of fractions and
mixed numbers by April of Grade 7. (which is the time of the Grade-7 state
test) The problems below are intended to be done without a calculator.
Of course, the whole-number arithmetic involved should be in line with the
degree of complexity the Standards assign to whole-number arithmetic without
a calculator. This being said, it is also important that some moderately
large whole numbers appear in numerators or denominators so that students
come to understand that there are some very general principles underlying
specific calculations, especially as a preparation for algebra since in algebra
the general principles are often the focus.

Notice that I have said these problems are for Grades 3-7, or possibly
2-7, even though, according to the Standards, it is only in Grades 5-7 that
arithmetic with fractions and mixed numbers is regarded as relevant for the
state tests. There is no inconsistency here. For state test readiness, which is
the focus of the Standards, it is important that students develop skills over
several years, especially in such a vast subject as arithmetic with fractions.

Prime numbers and least common multiples play a central role in adding
and subtracting fractions and greatest common divisors are relevant for reducing
fractions to lowest terms. Some problems involving prime numbers,
least common multiples, and greatest common divisors are included below.

This link is focused on the arithmetic of fractions and mixed numbers.
It might be that a future link will treat this arithmetic in conjunction with
problems in context, but such problems are not included here.

Also, this link does not directly treat the meaning of fractions. My
impression is that materials adopted for consistency with the pre-2003 standards
give this topic appropriate emphasis.

Teachers and others should feel free to download this list and possibly cut
off a bottom portion of the list in order to avoid showing younger children
problems far beyond what they can do and/or cut off a top portion of the
list to avoid giving the impression to older children that arithmetic with
fractions is trivial.

I use the term ‘mixed number’ even though ‘mixed numeral’ would be
more accurate; and I speak of ‘proper’ and ‘improper’ fractions, even though
here these adjectives have meanings that are unrelated to the meanings they
have in ordinary discourse. Also, when fractions are studied, the phrase ‘is
equivalent to’ is often used synonomously with ‘is equal to’ and ‘equals’—
and similarly for the variations which are used as adjectives.

This list of problems is focused on certain skills. It does not treat meanings
of fractions or reasons why certain operations work the way they do;
these are also important, but they are not treated in this list of problems.
However, my view is that, as a side benefit, honing of skills often increases
understanding.

I am not involved in the construction of the state math tests, known as
MCA’s, for 2006. Thus, I cannot speak about the extent, if any, to which
skill on the problems below will be useful preparation for the 2006 MCA’s.
However, I have kept the 2003 State Mathematics Standards in mind as I
have written these exercises.

1. Calculate the sums:

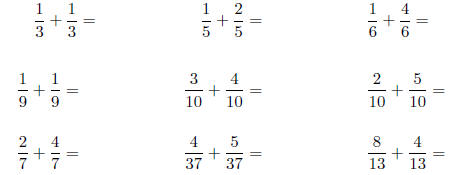
2. Calculate the following differences:

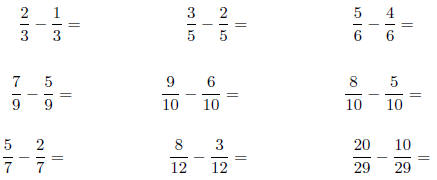
3. Write each whole number as a fraction with denominator 3:
3 =
8 =
1 =
10 =
200 =
15 =

4. Write each of the following mixed numbers as an improper fraction with
denominator 4:

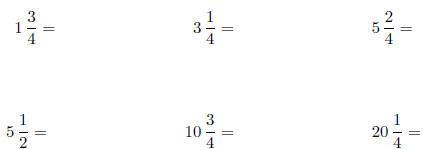
5. Reduce the following fractions to lowest terms (meaning write an equivalent
fraction that has as small a denominator as possible):

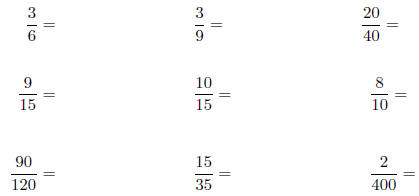
6. Find equivalent fractions having denominator 12 for each of the following
fractions:

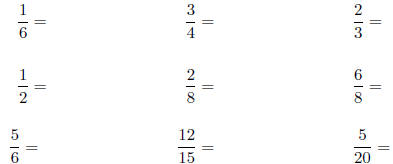
7. Reduce the following improper fractions to lowest terms (meaning write
an equivalent improper fraction that has as small a denominator as possible):

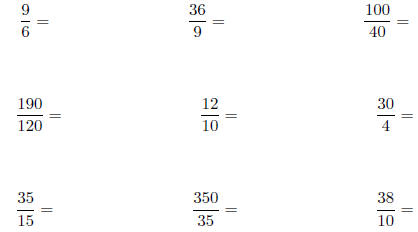
8. Find equivalent improper fractions having denominator 8 for each of the
following improper fractions:

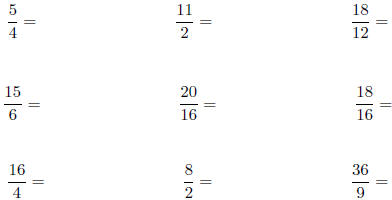
9. Calculate each of the following sums and write the answer as a fraction
(possibly improper) in lowest terms (that is with the smallest possible
denominator which might equal 1 sometimes):

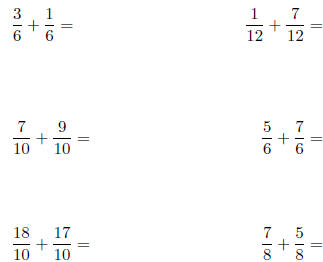
10. Calculate each of the following differences and write the answer as
a fraction (possibly improper) in lowest terms (that is with the smallest
possible denominator which might equal 1 sometimes):

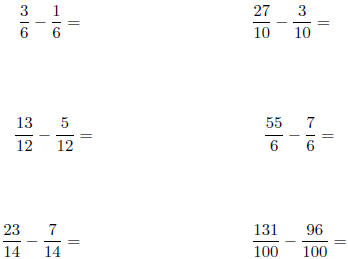
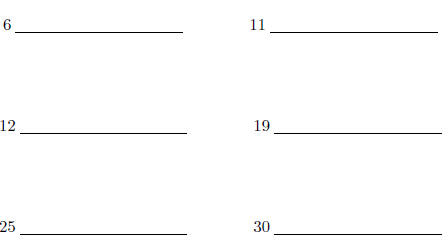
11. Decide whether each of the following numbers is prime or composite. If
it is composite write it as the product of prime numbers.

12. Calculate the following products:

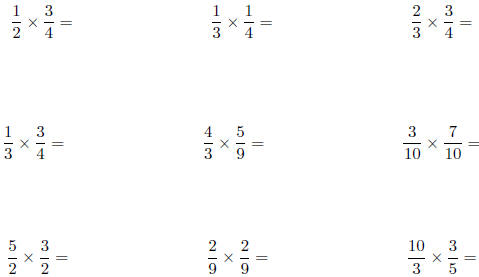
13. Decide which answers for the preceding problem are in lowest terms.
For those that are not, reduce them to lowest terms, keeping in mind that
a whole number can be written as a fraction in lowest terms by using a
denominator of 1.

14. Calculate the following quotients:

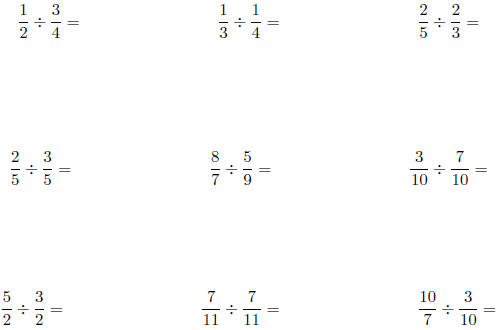
15. Decide which answers for the preceding problem are in lowest terms.
For those that are not, reduce them to lowest terms