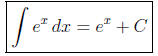The Natural Exponential Function

The definition. The natural logarithm function ln x is an increasing function whose domain
is the open interval (0,∞) and whose range is R, all of the real numbers. Since it’s increasing,
therefore it’s one-to-one and has an inverse, the natural exponential function, which we denote
exp x. Soon we’ll also denote it e^x, but as that notation already has a meaning when x is a
rational number, we’ll have to show exp x agrees with e^x for rational x.

Now, exp is inverse to ln, and that means

exp x = y iff x = ln y.

Let’s start by showing exp(m/n) = e^m/n for rational numbers m/n so we can use the
usual exponential notation. We know that

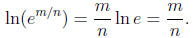
But since exp is inverse to ln, that statement is equivalent to

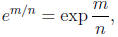
which is what we wanted to show.

Now we can use the usual exponential notation, but be aware that exp is still used when
the exponent is complicated. For instance, a notation like is preferred by many
over .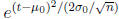

Properties of the natural exponential function. That the natural exponential function
is inverse to the natural log now reads

From this logical equivalence, every statement about ln can be converted to a statement
about e^x.

Here’s a table with properties of ln and exp.

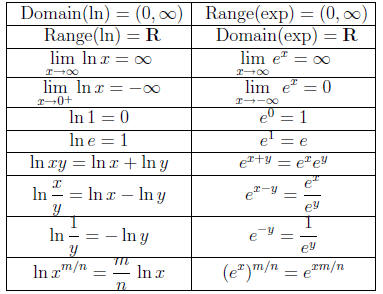
The first few lines in the table are direct translations of the properties of ln into properties
of exp. The later ones are almost direct, but not quite. For example, let’s see how the identity
ln xy = ln x+ln y implies the identity 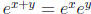. It would help to change the variables in one
of the identities since they don’t exactly correspond. Let’s show the identity ln xy = ln x+ln y
implies the identity .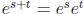

Let s = ln x so that x = e^s, and let t = ln y so that y = e^t. Since ln xy = ln x + ln y,
therefore s + t = ln x + ln y = ln xy. That implies 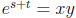, which equals e^se^t, and that was
what we wanted to show.

Note that the final equation in the right column of the table, 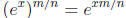is not quite
satisfactory. We would prefer to have 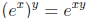for any real number y, not just for rational
y = m/n, but we haven’t yet defined what 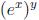would mean since we have only defined
exponentiation when the base is e, not when the base is an arbitrary real number like e^x.
That comes soon.

The derivative and integral of the natural exponential function. Recall that, for
positive x, 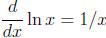, that is, 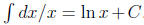. Let’s use that information to determine
the derivative and integral of e^x. We’ll use the inverse function theorem for derivatives to to
that.

The inverse function theorem says that if y = f(x) so that x = f ^-1(y), then

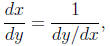
that is,

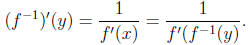
Right now, we have y = f(x) = ln x, x = f ^-1(y) = e^y, and f'(x) = 1/x. We want to find the
derivative of e^y, that is, 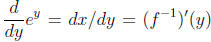. By the inverse function theorem, that
equals

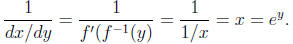
Thus, the derivative 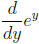of the exponential function e^y is itself e^y. If we switch to x as the
independent variable, we can write this result as the exponential rule for derivatives

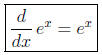
It is this property of the exponential function that gives it lots of applications in science.

Frequently, an exponential function has an exponent that is not just the variable x, but
a function of x, for instance 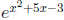. To find its derivative, use the exponential rule for
derivatives along with the chain rule: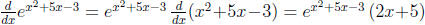
More generally,

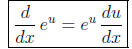
We can immediately use the exponential rule for derivatives, 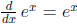, to integrate the
exponential function.