The California Mathematics Content Standards
Geometry Mathematics Content Standards
The geometry skills and concepts developed in this
discipline are useful to all students.
Aside from learning these skills and concepts, students will develop their
ability to
construct formal, logical arguments and proofs in geometric settings and
problems.
|
Note: The sample problems illustrate the standards and are written to help clarify them. Some problems are written in a form that can be used directly with students; others will need to be modified before they are used with students. |
1.0 Students demonstrate understanding by identifying
and giving examples of undefined terms, axioms, theorems, and inductive and deductive reasoning. Using what you know about parallel lines cut by a transversal, show that the sum of the angles in a triangle is the same as the angle in a straight line, 180 degrees. |
|
|
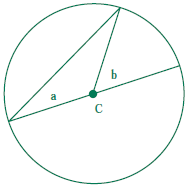
2.0 Students write geometric proofs, including proofs by contradiction. If C is the center of the circle in the figure shown below, prove that angle b has twice the measure of angle a.
|
||
|
3.0 Students construct and judge the validity of a logical argument and give counterexamples to disprove a statement. |
||
|
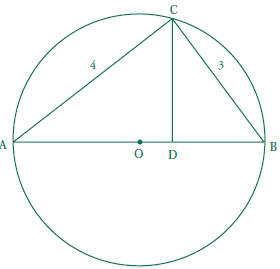
4.0 Students prove basic theorems involving congruence and similarity. AB is a diameter of a circle centered at O. CD ⊥ AB. If the length of AB is 5, find the length of side CD. (CERT forthcoming)
|
||
|
5.0 Students prove that triangles are congruent or similar, and they are able to use the concept of corresponding parts of congruent triangles. |
||
|
6.0 Students know and are able to use the triangle inequality theorem |
||
|
7.0 Students prove and use theorems involving the properties of parallel lines cut by a transversal, the properties of quadrilaterals, and the properties of circles. Prove that the figure formed by joining, in order, the midpoints of the sides of a quadrilateral is a parallelogram. |
||
|
8.0 Students know, derive, and solve problems involving the perimeter, circumference, area, volume, lateral area, and surface area of common geometric figures. |
||
|
9.0 Students compute the volumes and surface areas of prisms, pyramids, cylinders, cones, and spheres; and students commit to memory the formulas for prisms, pyramids, and cylinders. |
||
|
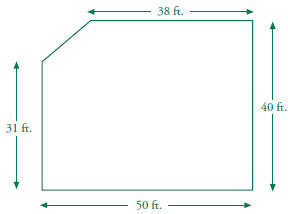
10.0 Students compute areas of polygons, including rectangles, scalene triangles, equilateral triangles, rhombi, parallelograms, and trapezoids. The diagram below shows the overall floor plan for a house. It has right angles at three corners. What is the area of the house? What is the perimeter of the house? (CERT 1997)
|
||
|
11.0 Students determine how changes in dimensions affect the perimeter, area, and volume of common geometric figures and solids. A developer makes a scale model of the tract house that she is going to build. Each inch of distance on the scale model corresponds to 30 inches on the actual houses. If the scale model uses 2 square feet of roofing material, how much roofing material will be needed for one of the actual houses? |
||
|
12.0 Students find and use measures of sides and of interior and exterior angles of triangles and polygons to classify figures and solve problems. |
||
|
13.0 Students prove relationships between angles in polygons by using properties of complementary, supplementary, vertical, and exterior angles.
In the figure below,
|
||
|
14.0 Students prove the Pythagorean theorem. |
||
|
15.0 Students use the Pythagorean theorem to determine distance and find missing lengths of sides of right triangles. |
||
|
16.0 Students perform basic constructions with a straightedge and compass, such as angle bisectors, perpendicular bisectors, and the line parallel to a given line through a point off the line. |
||
|
17.0 Students prove theorems by using coordinate geometry, including the midpoint of a line segment, the distance formula, and various forms of equations of lines and circles. |
||
|
18.0 Students know the definitions of the basic trigonometric functions defined by the angles of a right triangle. They also know and are able to use elementary relationships between them. For example, tan(x) = sin(x)/cos(x), (sin(x))2 + (cos(x))2 = 1. Without using a calculator, determine which is larger, tan (60°) or tan (70°) and explain why. |
||
|
19.0 Students use trigonometric functions to solve for an unknown length of a side of a right triangle, given an angle and a length of a side. Geometry |
||
|
20.0 Students know and are able to use angle and side relationships in problems with special right triangles, such as 30°, 60°, and 90° triangles and 45°, 45°, and 90° triangles. |
||
|
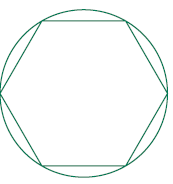
21.0 Students prove and solve problems regarding relationships among chords, secants, tangents, inscribed angles, and inscribed and circumscribed polygons of circles. Use the perimeter of a regular hexagon inscribed in a circle to explain why π > 3. (ICAS 1997)
|
||
|
22.0 Students know the effect of rigid motions on figures in the coordinate plane and space, including rotations, translations, and reflections. Geometry |



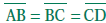 . Find an expression for the measure
of
. Find an expression for the measure
of