Math 0914 Exam 2
Directions: You have 90 minutes to answer
the following questions. You must show
all your work as neatly and clearly as possible and indicate the final
answer clearly. You
may use only a TI-30 calculator. The last page contains formulas that you might
find
useful. You may tear that page out.
If you are feeling ill you should inform the proctor. The proctor will note your
name and
Poly ID, and will accept any written statement(s) that you may wish to make
regarding
your illness.
| Problem | Possible | Points |
 |
||
| Total | 100 | |
(1) (Page 89, Problems 18, 21) A ball is thrown upward.
Its height (expressed in feet)
t seconds later is given by
h(t) = 96t - 16t2.
Show all your work, and include units in your answers.
(a) Evaluate and interpret h(4).
(b) Solve and interpret the equation h(t) = 96.
(c) When does the ball hit the ground?
(2) (Page 88, Problems 9-15) Find the quadratic function
whose roots are -1 and 2,
y-intercept is 2. Show all your work.
(3) (Page 99, Problems 113-120) Consider the following
system of equations
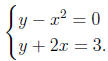
(a) Solve the system of equations for x and y. Show all your work.
(b) Graph the functions and show the solutions on the plane.
(4) (Page 109, Problem 25) At time t hours after taking
antibiotic ampicillin the
amount, A, in grams, remaining in the body is given by
A = 2.5 (0.84)t .
Fill in the blanks. You do not have to explain, but you must include units in
your
answers.
(a) The initial dose of ampicillin is  .
.
(b) The percentage of ampicillin that leaves the body each hour is
 .
.
(c) The amount of ampicillin left in the body 5 hours after the injection is
 .
.
(d) The time it takes until only 1.25 g of ampicillin remains in the body is
 .
.
(5) (Page 117, Problems 9-14) Find a possible formula for
the graph of the following
exponential function. Show all your work.
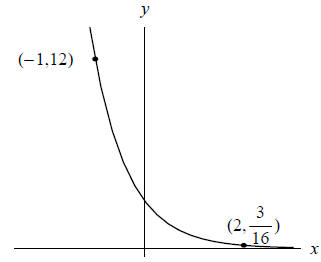
(6) (Page 134, Problems 29, 30) Determine which of the
functions given in the table be-
low is linear and which is exponential. Write formulas for the linear and
exponential
functions. Show all your work.
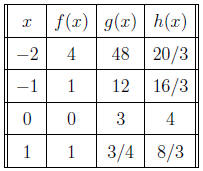
The linear function is  , and its formula is
, and its formula is
 .
.
The exponential function is  , and its formula is
, and its formula is
 .
.
(7) (Page 123, Problems 11-14, 20) Three exponential
functions are graphed in a figure
below. Six constants a, b, c, d, p and q determine these functions.
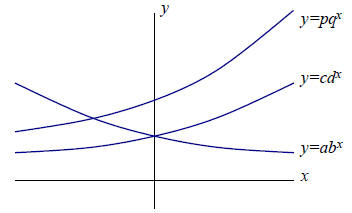
Answer the following questions. You do not have to
explain.
(a) Which of the constants are positive?
(b) Which of the constants are definitely between 0 and 1?
(c) Which of the constants are definitely greater than l?
(d) Which of the two constants are definitely equal?
(e) Which of the two constants COULD be equal?
a and p,
q and d.
(8) (Page 137, Problem 14-30) Determine weather each of
the following statements is
True or False. You do not have to explain.
(a) If a population increased by 50% each year, then in two years it increases
by
100%.
(b) If a > 1 in the formula Q = abt, then the graph always rises as we read from
left to right.
(c) In the formula Q = abt, the value a tells you where the graph crosses the
Q-axis.
(d) If P = 10e0.2t , we say the continuous growth rate of the function is 2%.
(e) Investing $1,000 for 30 years at 4% earns more if interest is compounded
monthly than if it is compounded annually.
(9) (Page 130, Problems 4-6) A population grows from its
initial level of 25,000 at a
continuous rate of 7.4% per year.
(a) Find a formula for P(t) the population in year t. Show all your work.
(b) By what percent does the population increase each year? Show all your work.
(10) (Page 142, Problem 104) Let h(t) = 1 + bt. Show that
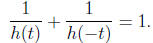
Useful formulas
• Factored form of a quadratic function:
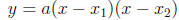
• Vertex form of a quadratic function:
y = a(x - h)2 + k


