Matrix Operations

THEOREM 2

Let A be m × n and let B and C have sizes for which the indicated sums and products are
defined.

a. A(BC) = (AB) C   (associative law of multiplication)
b. A (B + C) = AB + AC   (left - distributive law)
c. (B + C)A = BA + CA   (right-distributive law)
d. r(AB) = (rA)B = A (rB)
for any scalar r
e. 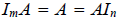(identity for matrix multiplication)

WARNINGS
Properties above are analogous to properties of real numbers. But NOT ALL real number
properties correspond to matrix properties.

1. It is not the case that AB always equal BA. (see Example 7, page 114)
2. Even if AB = AC, then B may not equal C. (see Exercise 10, page 116)
3. It is possible for AB = 0 even if A ≠ 0 and B ≠ 0. (see Exercise 12, page 116)

Powers of A

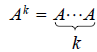
EXAMPLE.

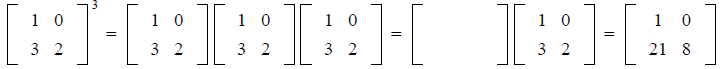
If A is m × n, the transpose of A is the n × m matrix, denoted by A^T, whose columns are formed
from the corresponding rows of A.

EXAMPLE.

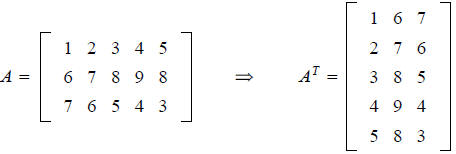
EXAMPLE: Let 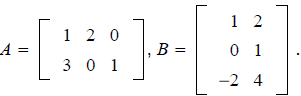Compute AB, (AB)^T, A^TB^T and B^TA^T.

Solution.

THEOREM 3

Let A and B denote matrices whose sizes are appropriate for the following sums and
products.

a. (AT) ^T = A (I.e., the transpose of A^T is A)
b. (A + B)^T = A^T B^T
c. For any scalar r, (rA)^T = rA^T
d. (AB)^T = B^TA^T (I.e. the transpose of a product of matrices equals the product of their
transposes in reverse order. )

EXAMPLE. Prove that (ABC)^T_________.

Solution. By Theorem 3d,

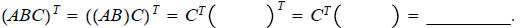
2.2 The Inverse of a Matrix

The inverse of a real number a is denoted by a ^-1. For example, 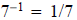and

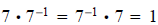
An n × n matrix A is said to be invertible if there is an n × n matrix C satisfying

CA = AC = I_n

where I_n is the n × n identity matrix. We call C the inverse of A .

FACT If A is invertible, then the inverse is unique.

Proof. Assume B and C are both inverses of A. Then

B = BI = B (_____) = ( ______) ______ = I______ = C.

So the inverse is unique since any two inverses coincide.
The inverse of A is usually denoted by A ^-1.

We have

Not all n × n matrices are invertible. A matrix which is not invertible is sometimes called a
singular matrix. An invertible matrix is called nonsingular matrix.

Theorem 4
Let
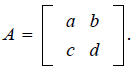If ad - bc ≠ 0, then A is invertible and

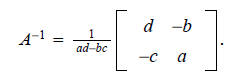
If ad - bc =  0, then A is not invertible.

Assume A is any invertible matrix and we wish to solve Ax = b. Then

_____Ax= _____b and so

Ix= _______ or x= _______.

Suppose w is also a solution to Ax = b. Then Aw = b and

_____Aw = _____b which means w = A^-1b.

So, w = A^-1b, which is in fact the same solution.

We have proved the following result.

Theorem 5
If A is an invertible n × n matrix, then for each b in Rⁿ, the equation Ax = b has the unique
solution x = A^-1b.

EXAMPLE. Use the inverse of A

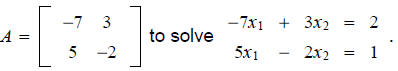
Solution. Matrix form of the linear system.

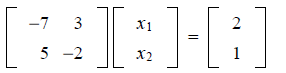
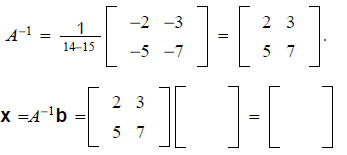
Theorem 6 Suppose A and B are invertible. Then the following results hold.
a. A ^-1 is invertible and (A^-1)^-1 = A (i.e. A is the inverse of A^-1).
b. AB is invertible and (AB)^-1 = B^-1A^-1
c. A^T is invertible and (A^T)^-1 = (A^-1)^T

Partial proof of part b.

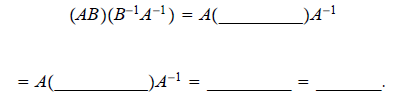
Similarly, one can show that (B^-1A^-1)(AB) =  I.

Theorem 6, part b can be generalized to three or more invertible matrices.
(ABC)^-1= __________

Earlier, we saw a formula for finding the inverse of a 2 × 2 invertible matrix. How do we find the
inverse of an invertible n × n matrix? To answer this question, we first look at elementary
matrices.

Elementary Matrices

Definition
An elementary matrix is one that is obtained by performing a single elementary row
operation on an identity matrix.

EXAMPLE. Let
 
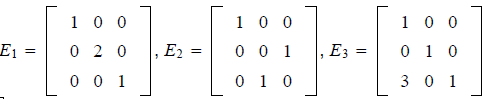
and

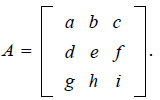
E₁, E₂, and E₃ are elementary matrices. Why?

Observe the following products and describe how these products can be obtained by elementary
row operations on A.

If an elementary row operation is performed on an m × n matrix A, the resulting matrix can be
written as EA, where the m × m matrix E is created by performing the same row operations on I_m.

Elementary matrices are invertible because row operations are reversible. To determine the
inverse of an elementary matrix E, determine the elementary row operation needed to transform
E back into I and apply this operation to I to find the inverse.

For example,

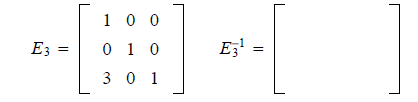
Example. Let 
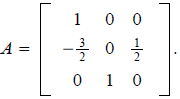. Then

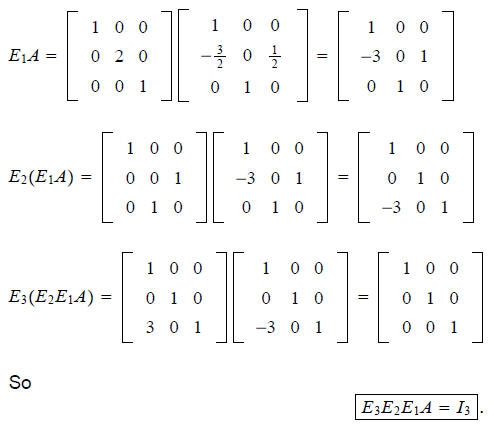
Then multiplying on the right by A^-1, we get
E₃E₂E₁A______= I₃______.

So
E₃E₂E₁I₃ = A^-1

The elementary row operations that row reduce A to I_n are the same elementary row
operations that transform I_n into A^-1.