Math 241 Homework Assignment 5

1. Prove that for all natural numbers, n,

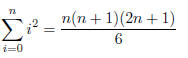
Solution

The proof is by induction on k with hypothesis

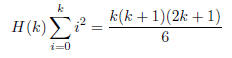
base case: To prove H(0),

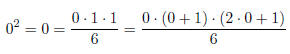
induction step: Assume H(k). Now,

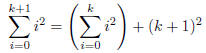	(expand)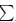
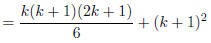	(IH)
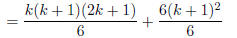	(multiply by 1 = 6/6)
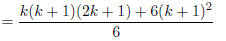	(add fractions)
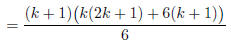	(factor (k + 1))
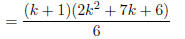	(combine like terms)
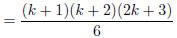	(factor 2k^2 + 7k + 6)
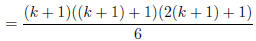	(arithmetic)

This completes the induction case and the proof of the problem.

2. Prove that for all natural numbers, n,

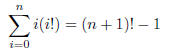
Solution

The proof is by induction on k with hypothesis

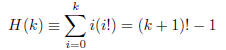
Recall that

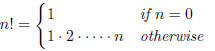
base case:

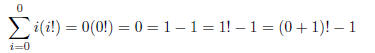
induction step: Assume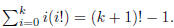Now,

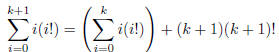	(expand)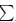
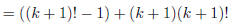	(induction hypothesis)
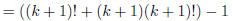	(rearrange sums)
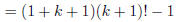	distribute (k + 1)!
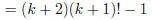	(simplify)
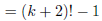	(meaning of ‘!’)
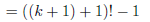	(as desired)

This proves H(k + 1) and completes the induction.

3. Prove that for all natural numbers n, 6 evenly divides n^3 − n.

Solution

The proof is by induction on k ∈N with hypothesis 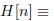“6 evenly devides n^3 − n”

Base Case (H[0]). 0^3 − 0 = 0, which is evenly divisible by 6.

Induction (H[k] ->  H[k + 1]). Assume that k^3 − k is evenly divisible by 6.

Now,

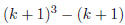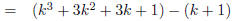	Expanding (k + 1)^3
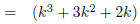	Combining like terms
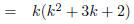	Distributing k
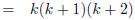	Factoring k^2 + 3k + 2

By Proposition A (below) this number is divisible by 3. And since at least one
of k, k + 1, or k + 2 is an even number, it is also divisible by 2. That is,
k(k + 1)(k + 2) = 2 · 3 · q, for some q, and is therefore divisible by 6.

Proposition A. For all n ∈ N, n(n + 1)(n + 2) is divisible by 3.

Proof: by induction on n with hypothesis, 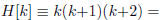3p for some p.

Base Case: 0 · 1 · 2 = 0 = 3 · 0.

Induction Case: Assume k(k + 1)(k + 2) = 3p for some p.

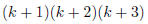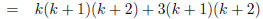		(distributing over k + 3)
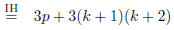		(Induction Hypothesis)
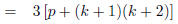		(distributing the 3)

Comment: It is reasonable to say that this proposition is obvious and need not be proven.

4. Prove that for all natural numbers n > 4, 2^n > n^2.

Solution

The proof is by induction on k with hypothesis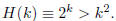

base case: To prove H(5),

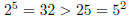
induction step: Assume 2^k > k^2. Now,

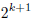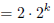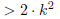		(induction hypothesis, used twice)

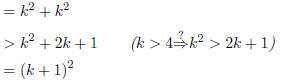The induction is finished once it is established that for any natural number n > 4,
n^2 > 2n + 1. This fact is proved in the lemma below.

lemma For all n > 3,n^2 > 2n + 1.

proof: The proof is by induction on k with hypothesis 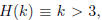k^2 >2k +1 .

base case:

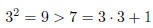
induction step: Assume k^2 > 2k + 1, k > 3. Then

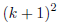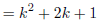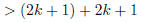		(induction hypothesis)
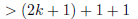		(k > 1)
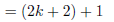		(arithmetic)
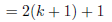		(arithmetic)

This completes the induction and the proof of the lemma.
The proof of the lemma completes the proof of the problem.

5. Hint: Solving this problem requires more than a straightforward algebraic derivation.
Think outside the box.

Prove that for all natural numbers n,

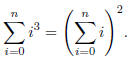
Solution

Solution Needed

6. Recall that the choose function, defined

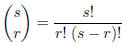
is the number of different ways to choose r objects from a set of s objects. Prove
that for all n ∈N,

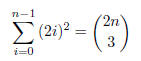
Solution

Solution needed.

7. For n ∈N, let Q, P₁, P₂, . . . , P_n be propositions. Prove the following:

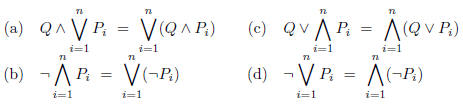
Solution

Solution Needed

8. Consider the program

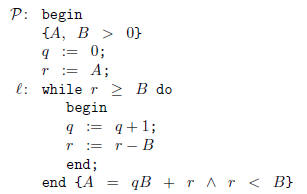
Use Theorem 4.2 and invariant assertion

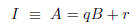
to prove that this program computes the quotient and remainder of A and B.

Solution

According to Theorem 4.2, it we can show that assertion I is true when P first
reaches 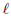and that executing the loop body leaves I true, then when P ends, I
will be true and the test “r≥B” will be false.

Thus, there are three things to prove: Note: Blue comments need not be included
because they are implied by the use of Theorem 4.2

1. Initialization (Base Case):

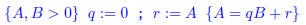
Since we have just assigned 0 to q and A to r we have
qB + r = 0 · B + A = A.

2. Invariance (Induction Case):

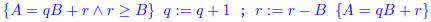
The loop body computes new values for program variables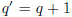and
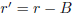(valid because r≥B). So we have

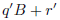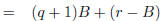		(substituting for r' and q')
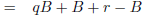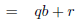		(simplifying)
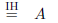		(assumption)

as desired.

3. Termination: It remains to show that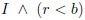implies the postcon-
dition,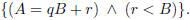But in this case the two formulas are
identical, so the implication is tautologically valid.

9. Supplemental Problem Comment: This is neither a calculus question nor
a logic puzzle

At last! You’ve gotten out of the dorms and into an apartment. Life can begin.
You get moved in and a few days later are looking for a brownie pan. When
you open the cabinet door, you see a 12-inch by 12-inch pan, just perfect for
your cooking needs. That’s the good news.

Unfortunately, there are four cockroaches in the pan, one at each corner. Now
you may not have known this, but cockroaches are very amorous creatures,
and will always move directly toward the object of their affection. Each of the
four in your pan is attracted to the one in the adjacent corner, going counterclockwise.
So all four cockroaches simultaneously start walking toward the one
that attracts them. As a result, they start spiraling toward the center of the
pan (See the diagram below).

Question: How far will the cockroaches travel?

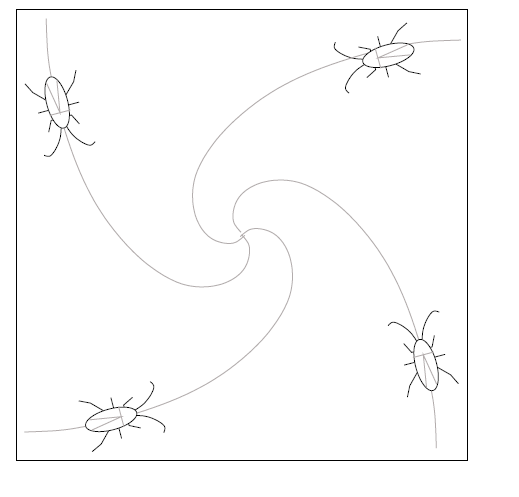
Solution

Each cockroach travels the length of one side of the square pan, 12 inches in the
problem as stated.

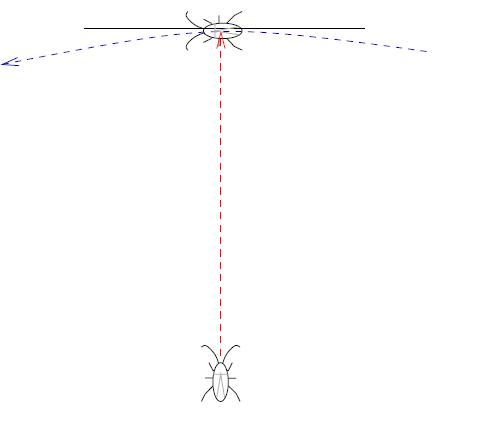
To gain the necessary insight, you have to look at the problem from the (any)
cockroach’s point of view. From that perspective,

(a) the cockroach is moving directly toward its target, perpendicular to the
(tangent) of the target’s path of travel. We know from geometry that this
is the shortest path it can take.

(b) We also know (from common sense), that the total distance a cockroach
travels is d = α + β, where α is the distance it has already traveled and
β is how far it has yet to go. When the cockroach takes a step, α and β
change by the same distance s, but d = (α + s) + (β − s) is is unchanged

These two properties are invariant—they do not change throughout cockroach’s
trip from the corner of the pan to its destination. From the cockroach’s point of
view, it is the pan that is turning, not itself. So by (a), above, it is invariantly
traveling along the shortest path to its destination; and the total distance (b) is
invariant also. Initially, d = 12 inches, so that is how far it travels.

Remark: The Comment at the beginning of the problem says that you don’t
need calculus to solve the problem, but this is not entirely true. What
you do need is a grasp of the underlying concepts of calculus. The
solution is only valid in the limit. The true distance is some multiple
of the number of discrete steps taken by the cockroach. Twelve
inches is the limit of that number as the length of each stride becomes
infinitesimal.¹

One can reasonably argue (as I suspect your Calculus instructor
would) that the “solution” given above needs to be verifyed by a
rigorous mathematical formulation by which the limit value can be
calculated. It is merely an idea about how to approach the proof.
It is worthwhile to set up that formulation. One the other hand, if
you were to write a program to approximate the limit, discovering
the problem’s invariants key to the computing the answer.

End Remark

¹Here’s an interesting fact about cockroaches. Most insects have two forms of locomotion
or gaits. One is walking in which two outer legs and to opposite middle leg work in unison.
The three legs act as a tripod, and the two tripods alternate, propelling the the insect forward
in a bi-pedal manner. The other gait is metachronal: the legs on either side thrust in sequence,
resulting in a “wave” traversing from front to back, like the legs of a centipede or caterpillar.
Cockroaches are unusual insects in that they have three gaits. In flight, a cockroach can
literally run on its two hind legs, keeping the other four raised off the ground.