Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

The Natural Exponential Function

Outline
1 The definition of the exponential function
2 exp is an exponential function
3 The derivative of e^x

Definition
ln, the natural logarithm, is an increasing function with domain (0,∞) and
range R. Let exp denote the inverse of ln; thus, exp has domain R and
range (0,∞).

Elementary properties of exp
• The graph of exp can be obtained directly from the graph of ln.
• We have the important inverse relationships:
ln(exp(x)) = x and exp(ln(x)) = x:

Euler's number, e
Recall the definition of e : exp is the number such that ln(e) = 1:
(e≈2.71828)

Theorem
exp(r ) = e^r for all rational numbers r :

Definition
• Because exp(r ) = e^r for all rational numbers, we will define e^x by
exp(x) for all real numbers x:
• In particular,
ln e^x = x and e^ln(x) = x.

Theorem (The laws of exponents)
• e^x+y = e^x e^y
• e^x-y = e^x/e^y (for homework)
• (ex)^r = e^rx (for homework)

Problem
Solve the following equations:
• e^2x-3 = 8
• e^2x + 2e^x - 8 = 0

Theorem

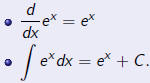
Problem
Find y' in each case:

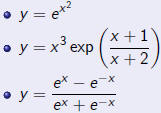
Problem
Solve the following integrals:

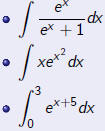
Problem
Sketch the graph of y = xe^-x.